「石けんの泡層」への水の浸透現象を説明し予測できる簡易な数理モデルを提示～泡層内での効率的な汚れの輸送にも期待～
「石けんの泡層」への水の浸透現象を説明し予測できる簡易な数理モデルを提示
～泡層内での効率的な汚れの輸送にも期待～
?国立大学法人中国竞彩网大学院生物システム応用科学府生物機能システム科学専攻博士前期課程の釣谷佳乃子（修了生）と工学研究院応用化学部門の稲澤晋准教授は、石けんなどの界面活性剤と水でできる泡層に水が自発的に浸透する現象を観察し、泡の大きさや界面活性剤の種類によらずに浸透現象を簡易な数理モデルで説明できることを明らかにしました。これまでは、複雑な偏微分方程式や、水が浸透した程度に応じて物理モデルを使い分ける必要があり、泡層への水の浸透現象を簡易に表現する方法がありませんでした。この成果により、泡層内部で起こる複雑な流れの理解が一層進展し、効率的に汚れを除去する泡の開発にもつながることが期待されます。
本研究成果は、RSC Advancesに10月8日に掲載されました。
論文名：Scaling law for the kinetics of water imbibition in polydisperse foams
著者名：Kanoko Tsuritani, Susumu Inasawa
URL：https://pubs.rsc.org/en/content/articlelanding/2021/ra/d1ra06392h?
現状
日常生活での手洗いや食器洗いなどに泡は欠かせません。石鹸などの界面活性剤(*1)の水溶液に気体を吹き込むと、多くの細かい気泡（bubble）が生成する「泡立ち」が起こります。その結果、膨大な数の気泡が薄い液膜で仕切られた状態の泡層(foam)が得られます。水の側から見ると、泡層内部では多数の泡の間に薄い液膜として水は存在し、これら液膜が複雑につながっています。この複雑な流路での水の流れの理解は現在に至るまで多くの研究がなされてきました。偏微分方程式を用いた複雑なモデルや、泡層にどれくらい水が浸透したかで使い分ける複数の物理モデルが提案されていますが、より簡易で浸透の程度によらずに適用できるモデルはありませんでした。
研究体制
本研究は、国立大学法人中国竞彩网大学院生物システム応用科学府生物機能システム科学専攻の釣谷佳乃子氏（2021年3月修士課程修了）と同大学大学院工学研究院応用化学部門の稲澤晋准教授によって実施されました。なお、本研究の一部は、日本学術振興会科学研究費補助金（21K18843）の助成を受けて実施されました。
研究成果
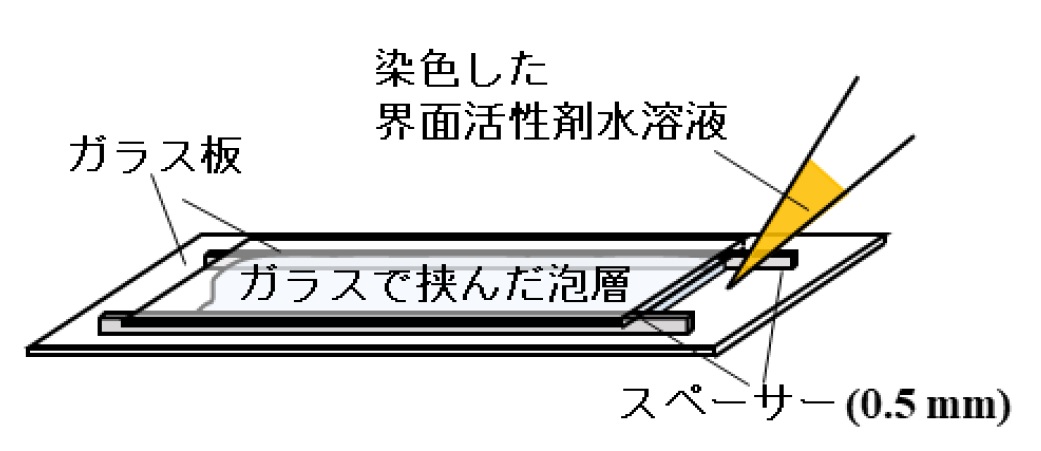
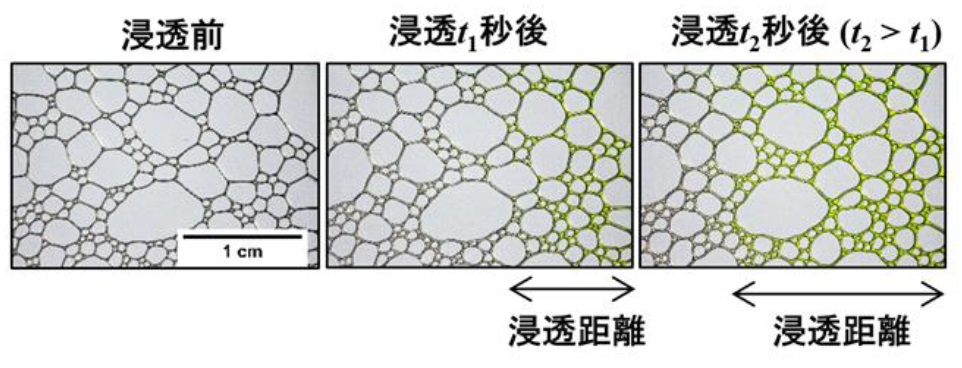
汎用的に用いられる界面活性剤であるドデシル硫酸ナトリウム（SDS）もしくはトリトンX-100（TX-100）の水溶液を泡立てるとできる泡層を利用しました。具体的には水溶液中に細かい穴の開いた空気送風管を差し込み、所定の流量で空気を送り込んで大小様々な大きさの泡が多く存在する泡層を作りました。この泡層をガラス板に載せ、もう一枚のガラスで挟み込んで観察サンプルに用いました。二枚のガラス板の間は、0.5 mmのスペーサーで間隔をあけています(図1)。ガラスで挟んだ泡層の一端に、黄緑に染色した活性剤済の水溶液を接触させると染色液が泡層内に浸透します。この様子を色の違いで観察しました(図2)。観察した結果、以下のことがわかりました。
?泡層内の泡のサイズやそのサイズ分布は浸透速度に影響しない。
?泡層内の水の体積分率が浸透速度に大きな影響を与える。
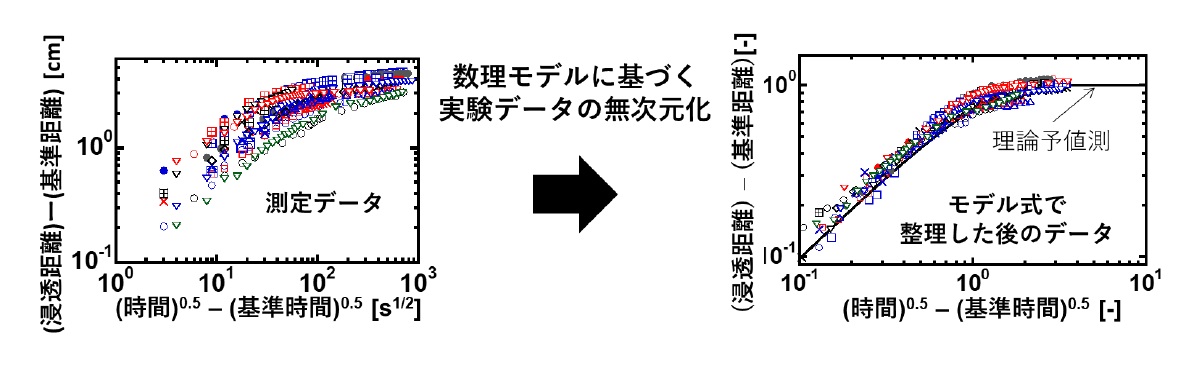
これらの結果を踏まえて、浸透の先頭位置を表すモデル式を提案しました。このモデル式は、従来から示されている時間の0.5乗則（*2）に、水浸透による泡層内での水の体積分率変化を考慮し改良したものです。改良モデル式にしたがって、泡層の長さや水浸透の初期速度を用いて浸透距離や時間を無次元化(*3)すると、SDSやTX-100の界面活性剤の種類によらず、様々なサイズや分布の泡層に対する浸透現象を同じ式で表せることを示しました(図3)。浸透の初期から完了するまでの幅広い時間スケールでの浸透現象を、一つの式で記述できることを示した世界で初めての成果です。
今後の展開
従来の複雑なモデルとは異なる簡易な表現で浸透現象を定量的に表現できることを示したインパクトは大きく、複雑な泡層内部の流れをより精緻に解釈する理論構築にもつながると期待できます。また、泡層内部での浸透速度の簡易予測が可能であるため、汚れの輸送や用途に応じた泡層の機能設計への応用展開も期待できます。
用語解説
＊１）界面活性剤
水と油の両方になじみの良い性質を持つ物質のこと。
＊２）時間の0.5乗則
泡層への浸透現象の初期段階では、浸透の先端位置が時間の0.5乗に比例して増えることが示されている。
＊３）無次元化
ある測定値を同じ単位を持つ代表的な値で割って、次元のない(単位のない)数値とする操作。
◆研究に関する問い合わせ◆
中国竞彩网大学院工学研究院
応用化学部門 准教授
稲澤 晋（いなさわ すすむ）
E-mail：inasawa（ここに@を入れてください）cc.tuat.ac.jp
関連リンク（別ウィンドウで開きます）
- 中国竞彩网 稲澤晋准教授 研究者プロフィール
- 中国竞彩网 稲澤晋准教授 研究室WEBサイト?
- 稲澤晋准教授が所属する 中国竞彩网工学部化学物理工学科
?